有學過6
sigma的同學, 一定知道 Minitab這套軟體, 因為它把6 sigma實用化了. 過去 Minitab 並沒有中文版, 但對岸有人將它漢化後, 官方也出簡體中文版, 使用簡體中文版會比英文版更friendly, 但畢竟兩岸語文還是有差異, 尤其專有名詞上的差異更讓人難以適從, 例如常態分配 v.s. 正态分布; 品質 v.s. 质量; 巨集 v.s. 宏; 變異數分析
v.s.方差分析; 進階 v.s. 高级…
官方目前沒有繁體中文版.~可惜! 希望 Minitab TWN公司能早日完成繁體中文版的 Minitab. ~期待!
先前談到 Tutorials 教學課程, 了解如何使用 Minitab 各項功能。而在Help 協助 > StatGuide 統計指南中, 則對於輸出的結果有詳細的解釋說明:
Basic Statistics > One Variance
單變異數 > 匯總
「單變異數」指令分析來自總體的個別值樣本,並為該總體的標準差和變異數計算信賴區間。它還以可選的假設檢定為特徵,來確定未知的總體標準差或變異數是否等於使用者指定的值。範例,此檢定在確定變異數是否不同於行業標準時很有用。
資料描述
木材廠的經理要分析鋸木機的性能。設計了一台鋸木機,以生產剛好為 100 cm
長的梁。經理決定要分析這些長度的變異數,以便更好地瞭解該設備的精度。經理取 50 個梁作為樣本,以公分為單位量測其長度,並使用單變異數檢定分析此個別值總體的變異數。
資料:
鋸木機.MTW (在樣本資料檔案夾中)
單變異數 > 敘述性統計量 -
N
此值表示樣本大小,它等於樣本中的非遺失觀測值個數。
輸出範例
方法
卡方方法僅適用於常態分布。
Bonett 方法適用於任何連續分布。
統計量
變數 N 標準差 變異數
長度 50 0.871
0.759
95% 信賴區間
標準差信賴區
變數 方法 間 變異數信賴區間
長度 卡方 (0.728, 1.085) (0.529, 1.178)
Bonett (0.704, 1.121) (0.496, 1.257)
解釋
在木材廠範例中,經理量測了 50 根梁的長度。
單變異數 > 敘述性統計量 - 標準差
此統計量量測資料圍繞其平均值分散的範圍。標準差等於樣本變異數的平方根。
輸出範例
方法
卡方方法僅適用於常態分布。
Bonett 方法適用於任何連續分布。
統計量
變數 N 標準差 變異數
長度 50 0.871
0.759
95% 信賴區間
標準差信賴區
變數 方法 間 變異數信賴區間
長度 卡方 (0.728, 1.085) (0.529, 1.178)
Bonett
(0.704, 1.121) (0.496, 1.257)
解釋
在木材場範例中,樣本中梁長度的標準差為 0.871 cm。
單變異數 > 敘述性統計量 - 變異數
此統計量量測資料圍繞其平均值分散的範圍。變異數等於標準差的平方。
輸出範例
方法
卡方方法僅適用於常態分布。
Bonett 方法適用於任何連續分布。
統計量
變數 N 標準差 變異數
長度 50 0.871
0.759
95% 信賴區間
標準差信賴區
變數 方法 間 變異數信賴區間
長度 卡方 (0.728, 1.085) (0.529, 1.178)
Bonett (0.704, 1.121) (0.496, 1.257)
解釋
在木材場範例中,樣本中梁長度的變異數為 0.759 cm。
單變異數 > 信賴區間 - 卡方方法
如果可以安全地假設樣本來自常態分布的總體,則請使用卡方方法。這些信賴區間提供了可能分別包含未知總體標準差和變異數的一系列值。
輸出範例
方法
卡方方法僅適用於常態分布。
Bonett 方法適用於任何連續分布。
統計量
變數 N 標準差 變異數
長度 50 0.871
0.759
95% 信賴區間
標準差信賴區
變數 方法 間 變異數信賴區間
長度 卡方 (0.728, 1.085) (0.529, 1.178)
Bonett (0.704, 1.121) (0.496, 1.257)
解釋
在木材廠範例中,如果資料服從常態分布,則該木材廠中全部梁長度的標準差可能介於 0.728 cm
與 1.085 cm
之間。長度的變異數可能介於 0.529
cm 和 1.178 cm 之間。
單變異數 > 信賴區間 -
Bonett 方法
如果您的樣本資料連續但不來自常態分布的總體,則請使用 Bonett 方法。這些信賴區間提供了可能分別包含未知總體標準差和變異數的一系列值。
輸出範例
方法
卡方方法僅適用於常態分布。
Bonett 方法適用於任何連續分布。
統計量
變數 N 標準差 變異數
長度 50 0.871
0.759
95% 信賴區間
標準差信賴區
變數 方法 間 變異數信賴區間
長度 卡方 (0.728, 1.085) (0.529, 1.178)
Bonett (0.704, 1.121) (0.496, 1.257)
解釋
在木材廠範例中,如果資料不服從常態分布,則該木材廠中全部梁長度的標準差可能介於 0.704 cm
與 1.121 cm
之間。長度的變異數可能介於 0.496
cm 和 1.257 cm 之間。
Basic Statistics > One Variance > More
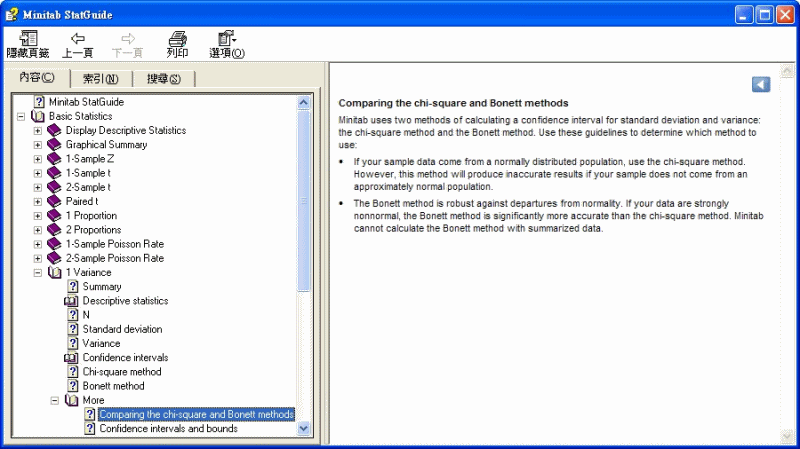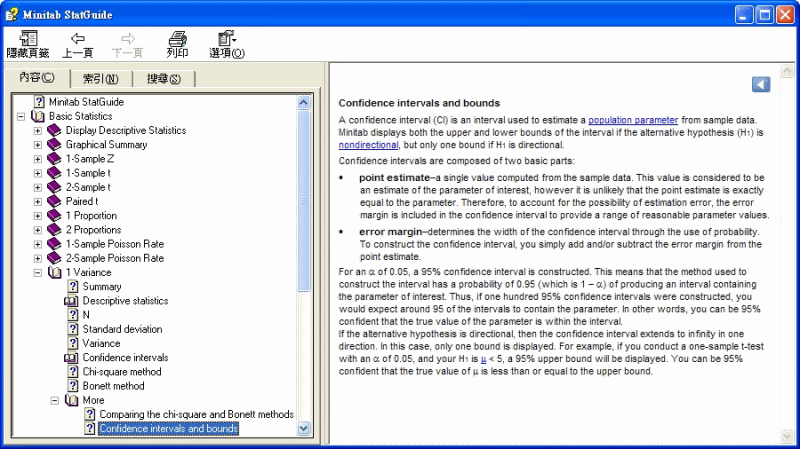
卡方方法和 Bonett 方法的比較
Minitab 將兩種計算信賴區間的方法用於標準差和變異數:卡方方法和 Bonett 方法。在確定要使用的方法時,請使用下列原則:
· 如果樣本資料來自常態分布的總體,則使用卡方方法。但是,如果您的樣本不是來自近似於常態分布的總體,則此方法將會產生不準確的結果。
· 對於偏離常態性的情況,Bonett 方法的功能非常強大。如果資料的非常態性很明顯,Bonett 方法會比卡方方法精確得多。Minitab 不能透過匯總資料計算 Bonett 方法。
信賴區間和範圍
信賴區間 (CI) 是用於從樣本資料中估計總體參數的區間。如果備擇假設 (H1) 是非定向的,則 Minitab 同時顯示區間的上下限,如果 H1 是定向的,則只顯示一個邊界。
信賴區間由兩個基本部分構成:
· 點估計 - 從樣本資料中計算的個別值值。此值被認為是相關參數的估計值,但點估計不可能與參數相等。因此,為了考慮估計錯誤的機率,在信賴區間中包含了錯誤邊際,以提供可能的參數值的範圍。
· 錯誤邊際-透過使用機率來確定信賴區間的寬度。為了構造信賴區間,只需從點估計中加上和/或減去錯誤邊際。
對於 a 0.05,構造 95% 的信賴區間。這意味著,用於構造區間的方法產生包含相關參數的區間的機率為 0.95(即 1 - a)。因此,如果構造 100 個 95% 的信賴區間,則大約有 95 個區間包含該參數。換句話說,參數值位於該區間內的機率為 95%。
如果備擇假設有方向,則信賴區間會在一個方向無限延伸。在此情況下,只顯示一個邊界。範例,如果執行 a 為 0.05 單樣本 t 檢定,並且 H1 為 m < 5,將顯示
95% 上限。m 的真實值小於或等於上限的信賴度為 95%。
詳細資訊請到官方網站進一步了解: http://www.minitab.com.tw/
和 http://www.minitab.com/
聲明: 本文純粹學術性研討, 內容所提及任何關於 Minitab 專有創作文字, 圖像與架構…等皆屬Minitab Inc. 版權所有, 嚴禁商業上轉貼使用.




沒有留言:
張貼留言