有學過6
sigma的同學, 一定知道 Minitab這套軟體, 因為它把6 sigma實用化了. 過去 Minitab 並沒有中文版, 但對岸有人將它漢化後, 官方也出簡體中文版, 使用簡體中文版會比英文版更friendly, 但畢竟兩岸語文還是有差異, 尤其專有名詞上的差異更讓人難以適從, 例如常態分配 v.s. 正态分布; 品質 v.s. 质量; 巨集 v.s. 宏; 變異數分析
v.s.方差分析; 進階 v.s. 高级…
官方目前沒有繁體中文版.~可惜! 希望 Minitab TWN公司能早日完成繁體中文版的 Minitab. ~期待!
先前談到Assistant
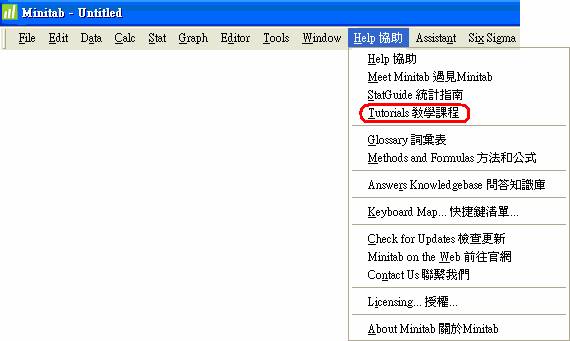
助手, 可幫助我們選擇正確工具進行分析, 並告訴我們如何解釋結果. 現在更進一步, 我們可透過Help 協助
> Tutorials 教學課程, 了解常用統計功能的”用途”;”資料”;”操作步驟”,同學可利用minitab所附範例, 熟悉此功能的操作, 至於輸出的解釋, 後面會在Help 協助 > StatGuide 統計指南 中討論.
Basic Statistics > 2-Sample Poisson Rate > Uses
用途: 雙樣本 Poisson 率
用法 1: 確定兩個組之間是否存在比例差異
一家紡織品製造商使用兩台紡織機來生產最暢銷的織物。
它希望確保這兩台機器之間不存在品質差異。 因為此製造商正在量測瑕疵率(每 10 碼材料中的織物瑕疵數),所以,此資料遵循 Poisson 分布。
有時,您只需知道存在有實際意義的差異即可。
透過 Poisson 資料,您可以使用雙樣本 Poisson 率檢定比較兩個組的比例。
用法 2: 確定一組中發生某個事件的比例是否比另一組高
兩位工藝控制工程師分別想出了安裝電視玻璃螢幕時盡可能少地產生劃痕的方法。
公司希望知道哪種方法所生產的劃痕率更低。
請使用雙樣本 Poisson 率檢定來確定某一組的發生率是否比另一組高。
用法 3: 確定兩組的比例差異是否為某一特定量
一家印刷公司考慮取代其印刷機以減少缺點印刷件的數量。
但是,僅當缺點比例降低 5% 或更多時才值得對此次設備升級投資。
即使兩組之間存在比例差異,差異可能會因為太小而沒有任何實際意義。
透過雙樣本 Poisson 率檢定,您可以檢定您認為重要的任意大小之間的差異,並計算出可能會包含組間差異的一系列值。
Basic Statistics > 2-Sample Poisson Rate > Data
資料: 用於雙樣本 Poisson 率的資料
需要什麼類型的資料?
資料必須遵循 Poisson 分布。 也就是說,它們必須表示事件數、缺點數或現行數。 此外,資料必須為非負整數。 範例:
每天經過兩個不同人列橫道的列人數量
每個班次在兩條塗裝線上生產的汽車新油漆塗層上的缺點數
每小時在兩個呼叫區域中的 911 來電數
請考慮您需要多少資料才能確保檢定具有足夠的功效檢測出兩個組間的差異。
為了協助確定所需的樣本大小,請使用統計 > 功效和樣本數量 > 雙樣本 Poisson 率。
我的工作表的外觀如何?
原始資料
原始資料可以是堆疊資料,也可以是未堆疊資料。
要輸入堆疊的原始資料,請在一欄中欄出這兩個樣本的觀測值,然後提供另一個下標欄來標識樣本。
|
|
C1
|
C2
|
|
|
缺點數
|
下標
|
|
1
|
1
|
夜間
|
|
2
|
3
|
夜間
|
|
3
|
2
|
夜間
|
|
4
|
0
|
夜間
|
|
5
|
1
|
夜間
|
|
6
|
5
|
日期
|
|
7
|
4
|
日期
|
|
8
|
6
|
日期
|
|
9
|
5
|
日期
|
要輸入未堆疊的原始資料,請在一欄中欄出每個樣本中的每個觀測值。
|
|
C1
|
C2
|
|
|
夜間
|
日期
|
|
1
|
1
|
5
|
|
2
|
3
|
4
|
|
3
|
2
|
6
|
|
4
|
0
|
5
|
|
5
|
1
|
|
頻數資料
頻數資料可以是堆疊資料,也可以是未堆疊資料。
要輸入堆疊的頻數資料,請在一欄中欄出來自這兩個樣本的唯一值。
在另一個欄中欄出下標來標識每個觀測值的樣本。 最後,在第三個欄中欄出每個唯一值的頻數。
|
|
C1
|
C2
|
C3
|
|
|
缺點數
|
下標
|
頻數
|
|
1
|
0
|
夜間
|
2
|
|
2
|
1
|
夜間
|
2
|
|
3
|
2
|
夜間
|
1
|
|
4
|
1
|
日期
|
1
|
|
5
|
4
|
日期
|
3
|
|
6
|
5
|
日期
|
1
|
要輸入未堆疊的頻數資料,請在一個單獨的欄中欄出來自每個樣本的唯一值,然後在另外兩個欄中欄出它們的頻數。
|
|
C1
|
C2
|
C3
|
C4
|
|
|
夜間
|
頻數_夜間
|
日期
|
頻數_日期
|
|
1
|
0
|
2
|
1
|
1
|
|
2
|
1
|
2
|
4
|
3
|
|
3
|
2
|
1
|
5
|
1
|
匯總資料
要輸入匯總資料,工作表中不需要資料。
只需在對話框中鍵入發生次數和每個樣本的樣本大小即可。 對於 Poisson 資料,樣本大小等於對專案計數的單位數。
範例,如果您對兩條生產線記錄了 30 天的缺點數,則樣本大小將為 30。
Basic Statistics > 2-Sample Poisson Rate > How To
操作步驟: 在 Minitab 中執行雙樣本
Poisson 率檢定
方案
您是郵政服務的分析員,您要對兩個郵局分支機構進行比較,以確定哪個機構的客戶每日到訪率更高。
您對 40 個工作日內(上午 9:00 - 下午 5:00)進入每個分支機構的客戶數進行統計,並使用雙樣本 Poisson 率函數比較每個分支機構的客戶到訪數。
選擇適當的分析方式
分析員希望分析兩個 Poisson 製程的比例之間的差異。 雙樣本 Poisson 率檢定是適用於此情況的檢定方式。
1.
開啟工作表“郵局.MTW”。
2.
選擇統計 > 基本統計量 > 雙樣本 Poisson 率。
輸入資料
此工作表中,每個樣本對應一欄原始資料。
1.
選擇樣本在不同欄中。
2.
在第一欄中,輸入'分支 A'。
3.
在第二欄中,輸入'分支 B'。
4.
點擊確定。
指定選項
此雙樣本 Poisson 率分析無需進一步修改,但您可以選擇其他選項。 使用選項子對話框可以請求單側檢定或變更信賴水準、檢定差異或每個樣本的觀測值長度。
(無需任何操作)
解釋輸出
現在應該做些什麼?
有關如何解釋此分析結果的指導資訊,請參見 StatGuide。
詳細資訊請到官方網站進一步了解: http://www.minitab.com.tw/
和 http://www.minitab.com/
聲明: 本文純粹學術性研討, 內容所提及任何關於 Minitab 專有創作文字, 圖像與架構…等皆屬Minitab Inc. 版權所有, 嚴禁商業上轉貼使用.






沒有留言:
張貼留言