Minitab: 6 sigma 專業軟體 繁體中文討論-116

有學過6 sigma的同學, 一定知道 Minitab這套軟體, 因為它把6 sigma實用化了. 過去 Minitab 並沒有中文版, 但對岸有人將它漢化後, 官方也出簡體中文版, 使用簡體中文版會比英文版更friendly, 但畢竟兩岸語文還是有差異, 尤其專有名詞上的差異更讓人難以適從, 例如常態分配 v.s. 正态分布; 品質 v.s. 质量; 巨集 v.s. 宏; 變異數分析 v.s.方差分析; 進階 v.s. 高级…

官方目前沒有繁體中文版.~可惜! 希望 Minitab TWN公司能早日完成繁體中文版的 Minitab. ~期待!

        先前談到 Tutorials 教學課程, 了解如何使用 Minitab 各項功能。而在Help 協助 > StatGuide 統計指南中, 則對於輸出的結果有詳細的解釋說明:

DOE > Taguchi > Analyze Taguchi Design

分析田口設計 > 匯總  

透過分析田口設計使用正交表來分析穩健性參數設計實驗的結果。使用所提供的圖表和表可以

·    瞭解控制因子、噪聲因子和信號因子如何影響反應

·    為產品或製程選擇因子設定的最佳組合

資料描述

多名科學家的興趣集中於研究五個因子對羅勒屬植物早期生長的影響。共有五個控制因子，每個因子有兩個水準。這些因子是：

·    植物的品種

·    光照量

·    肥料量

·    水量

·    噴灑農藥的頻率

科學家選擇了兩個噪聲因子，溫度和濕度，每個因子有兩個水準，然後將它們組合為四個噪聲條件。使用時間作為信號因子，這使得該實驗成為動態反應實驗。反應是葉子大小的量測值。科學家還檢定了品種與肥料之間的交互作用。實驗的目標是確定哪些因子設定在增加植物生長率（斜率）的同時不增加生長中的變異。

資料： 羅勒.MTW （在樣本資料檔案夾中）

分析田口設計 > 估計迴歸係數表 - P 值  

Minitab 將為所選擇的每個反應特徵都提供一個估計迴歸係數表。Minitab 為每個因子水準減一的水準計算係數。如果因子有三個水準，則係數對應於水準 1 和 2。如果因子有兩個水準，則係數對應於水準 1。

透過迴歸係數可以使用 p 值來確定哪個因子在統計意義上顯著。要使用 p 值，需要：

·    為要評估的因子確定 p 值。

·    將此 p 值與您的 a 水準進行比較。常用的 a 水準為 0.05。

-    如果該 p 值小於或等於 a，則描述效應顯著。

-    如果該 p 值大於 a，則描述效應不顯著。

輸出範例

信噪比 的模型係數估計

項                係數  係數標準誤差        T      P

常數            0.4401      0.2384    1.846  0.316

品種 1         -2.3667      0.2384   -9.926  0.064

光源 1         -1.1312      0.2384   -4.744  0.132

肥料 1         -4.5800      0.2384  -19.209  0.033

水 1           -1.4271      0.2384   -5.985  0.105

噴霧 1         -0.2127      0.2384   -0.892  0.536

品種*肥料 1 1  -0.6041      0.2384   -2.534  0.239

S = 0.6744   R-Sq = 99.8%   R-Sq（調整） = 98.7%

斜率 的模型係數估計

項                  係數  係數標準誤差       T      P

常數            0.715353     0.03796  18.846  0.034

品種 1         -0.028617     0.03796  -0.754  0.589

光源 1         -0.111020     0.03796  -2.925  0.210

肥料 1         -0.188904     0.03796  -4.977  0.126

水 1           -0.171643     0.03796  -4.522  0.139

噴霧 1         -0.008684     0.03796  -0.229  0.857

品種*肥料 1 1  -0.020446     0.03796  -0.539  0.685

S = 0.1074   R-Sq = 98.2%   R-Sq（調整） = 87.4%

標準差 的模型係數估計

項                 係數  係數標準誤差        T      P

常數            0.64182     0.01075   59.697  0.011

品種 1          0.13761     0.01075   12.799  0.050

光源 1         -0.09685     0.01075   -9.008  0.070

肥料 1          0.12592     0.01075   11.712  0.054

水 1           -0.11961     0.01075  -11.125  0.057

噴霧 1         -0.02108     0.01075   -1.961  0.300

品種*肥料 1 1   0.03966     0.01075    3.689  0.169

S = 0.03041   R-Sq = 99.8%   R-Sq（調整） = 98.7%

解釋

科學家計算了斜率、標準差和信噪比的迴歸結果。

·    對於信噪比，肥料 (0.033) 在 a 水準為 0.05 時顯著，而品種 (0.064) 在 a 水準為 0.10 時顯著。其餘因子不與反應顯著相關。

·    對於斜率，p 值表明在 a 水準為 0.05 或 0.10 時沒有因子是顯著的。

·    對於標準差，p 值表明品種 (0.050) 在 a 水準為 0.05 時顯著。肥料 (0.054)、水 (0.057) 和光照 (0.070) 在 a 水準為 0.10 時顯著。噴灑農藥 (0.30) 以及肥料與品種之間的交互作用 (0.169) 不顯著。

分析田口設計 > 估計迴歸係數表 - 係數  

Minitab 為每個因子水準減一的水準計算係數。如果因子有 3 個水準，則 Minitab 提供 2 個係數，對應於因子水準 1 和 2。如果因子有 2 個水準，則 Minitab 提供 1 個係數，對應於因子水準 1。Minitab 在因子旁邊包含對應於水準 1 的值或文字。係數的絕對值表示每個因子的相對長度。

在田口設計中，因子係數的量值通常反映反應表中的等級這一因子。係數絕對值最大的因子在反應表中等級為 1，係數絕對值第二大的因子在反應表中等級為 2，依此類推。

輸出範例

信噪比 的模型係數估計

項                係數  係數標準誤差        T      P

常數            0.4401      0.2384    1.846  0.316

品種 1         -2.3667      0.2384   -9.926  0.064

光源 1         -1.1312      0.2384   -4.744  0.132

肥料 1         -4.5800      0.2384  -19.209  0.033

水 1           -1.4271      0.2384   -5.985  0.105

噴霧 1         -0.2127      0.2384   -0.892  0.536

品種*肥料 1 1  -0.6041      0.2384   -2.534  0.239

S = 0.6744   R-Sq = 99.8%   R-Sq（調整） = 98.7%

斜率 的模型係數估計

項                  係數  係數標準誤差       T      P

常數            0.715353     0.03796  18.846  0.034

品種 1         -0.028617     0.03796  -0.754  0.589

光源 1         -0.111020     0.03796  -2.925  0.210

肥料 1         -0.188904     0.03796  -4.977  0.126

水 1           -0.171643     0.03796  -4.522  0.139

噴霧 1         -0.008684     0.03796  -0.229  0.857

品種*肥料 1 1  -0.020446     0.03796  -0.539  0.685

S = 0.1074   R-Sq = 98.2%   R-Sq（調整） = 87.4%

標準差 的模型係數估計

項                 係數  係數標準誤差        T      P

常數            0.64182     0.01075   59.697  0.011

品種 1          0.13761     0.01075   12.799  0.050

光源 1         -0.09685     0.01075   -9.008  0.070

肥料 1          0.12592     0.01075   11.712  0.054

水 1           -0.11961     0.01075  -11.125  0.057

噴霧 1         -0.02108     0.01075   -1.961  0.300

品種*肥料 1 1   0.03966     0.01075    3.689  0.169

S = 0.03041   R-Sq = 99.8%   R-Sq（調整） = 98.7%

解釋

羅勒資料的結果表明：

·    對於信噪比，由於肥料的係數 (-4.580) 最大，接下來依次是品種 (-2.3667)、水 (-1.4271)、光照 (-1.1312)、肥料與水的交互作用 (-0.6041) 以及噴灑農藥 (-0.2127)，因此肥料對反應的影響最大。

·    對於斜率，由於肥料的係數 (-0.188904) 最大，接下來依次是水 (-0.171643)、光照 (-0.111020)、品種 (-0.028617)、肥料與品種的交互作用 (-0.020446) 以及噴灑農藥 (-0.008684)，因此肥料對反應的影響最大。

·    對於標準差，由於品種的係數 (0.13761) 最大，接下來依次是肥料 (0.12592)、水 (-0.11961)、光照 (-0.09685)、肥料與品種 (0.03966) 的交互作用和噴灑農藥 (-0.02108)，因此品種對反應的影響最大。

分析田口設計 > 變異數分析表 - P 值  

使用變異數分析表中的 p 值確定模型中的哪些因子在統計意義上顯著。

要使用 p 值，需要：

·    為要評估的效應確認 p 值。

·    將此 p 值與您的 a 水準進行比較。常用的 a 水準為 0.05。

-    如果該 p 值小於或等於 a，則描述效應顯著。

-    如果該 p 值大於 a，則描述效應不顯著。

輸出範例

信噪比 的變異數分析

來源       自由度   Seq SS   Adj SS   Adj MS       F      P

品種            1   44.809   44.809   44.809   98.52  0.064

光源            1   10.236   10.236   10.236   22.51  0.132

肥料            1  167.811  167.811  167.811  368.97  0.033

水              1   16.293   16.293   16.293   35.82  0.105

噴霧            1    0.362    0.362    0.362    0.80  0.536

品種*肥料       1    2.920    2.920    2.920    6.42  0.239

殘差誤差        1    0.455    0.455    0.455

合計            7  242.886

斜率 的變異數分析

來源       自由度    Seq SS    Adj SS    Adj MS      F      P

品種            1  0.006551  0.006551  0.006551   0.57  0.589

光源            1  0.098603  0.098603  0.098603   8.55  0.210

肥料            1  0.285477  0.285477  0.285477  24.77  0.126

水              1  0.235690  0.235690  0.235690  20.45  0.139

噴霧            1  0.000603  0.000603  0.000603   0.05  0.857

品種*肥料       1  0.003344  0.003344  0.003344   0.29  0.685

殘差誤差        1  0.011527  0.011527  0.011527

合計            7  0.641795

標準差 的變異數分析

來源       自由度    Seq SS    Adj SS    Adj MS       F      P

品種            1  0.151490  0.151490  0.151490  163.82  0.050

光源            1  0.075040  0.075040  0.075040   81.15  0.070

肥料            1  0.126845  0.126845  0.126845  137.17  0.054

水              1  0.114456  0.114456  0.114456  123.77  0.057

噴霧            1  0.003556  0.003556  0.003556    3.85  0.300

品種*肥料       1  0.012581  0.012581  0.012581   13.61  0.169

殘差誤差        1  0.000925  0.000925  0.000925

合計            7  0.484893

解釋

羅勒資料的結果表明：

·    對於信噪比，肥料 (0.033) 在 a 水準為 0.05 時顯著，而品種 (0.064) 在 a 水準為 0.10 時顯著。其餘因子不與反應顯著相關。

·    對於斜率，p 值表明在 a 水準為 0.05 或 0.10 時沒有因子是顯著的。

·    對於標準差，p 值表明品種 (0.050) 在 a 水準為 0.05 時顯著。肥料 (0.054)、水 (0.057) 和光照 (0.070) 在 a 水準為 0.10 時顯著。噴灑農藥 (0.30) 以及肥料與品種之間的交互作用 (0.169) 不顯著。

科學家可能想要在不含交互作用項和噴灑農藥這一因子的情況下重新試驗分析，因為二者中任何一個對任何反應特徵都不顯著。

分析田口設計 > 反應表  

反應表提供：

·    設計中每個因子的每個水準的平均反應特徵

·    有助於評估哪些因子對要關心的反應特徵影響最大的等級和 delta 值。delta 值和等級解釋如下：

Delta：透過對每個反應特徵取最大值和最小值之差來量測效應的大小。

等級：按照對反應特徵的影響程度（基於 delta 值）從大到小排欄因子。

使用反應表選擇每個因子的最佳水準。通常，目標是使標準差盡可能小，使信噪比盡可能大，並滿足斜率的某些目標。使用 delta 和等級值確定對每個反應特徵影響最大的因子。然後，確定這些因子的哪些水準滿足您的目標。有時候，某個反應特徵的最佳因子水準與另一個反應特徵的最佳水準不同。要解決此問題，預測各種因子水準組合的結果以確定哪種組合產生的結果最佳會有所協助。

注意

 如果懷疑因子之間存在交互作用，則應檢查交互作用圖，以確保所選的因子水準組合是最佳的。

輸出範例

信噪比反應表

動態反應

水準      品種     光源     肥料       水    噴霧

1      -1.9266  -0.6911  -4.1399  -0.9870  0.2274

2       2.8068   1.5712   5.0201   1.8672  0.6527

Delta   4.7333   2.2623   9.1600   2.8542  0.4253

排列         2        4        1        3       5

斜率反應表

水準     品種    光源    肥料      水    噴霧

1      0.6867  0.6043  0.5264  0.5437  0.7067

2      0.7440  0.8264  0.9043  0.8870  0.7240

Delta  0.0572  0.2220  0.3778  0.3433  0.0174

排列        4       3       1       2       5

標準差反應表

水準     品種    光源    肥料      水    噴霧

1      0.7794  0.5450  0.7677  0.5222  0.6207

2      0.5042  0.7387  0.5159  0.7614  0.6629

Delta  0.2752  0.1937  0.2518  0.2392  0.0422

排列        1       4       2       3       5

解釋

羅勒資料的反應表顯示：

·    對於信噪比，肥料等級為 1，接下來是品種 (2)、水 (3)、光照 (4) 和噴灑農藥 (5)。

·    對於斜率，肥料等級為 1，接下來是水 (2)、光照 (3)、品種 (4) 和噴灑農藥 (5)。

·    對於標準差，品種等級為 1，接下來是肥料 (2)、水 (3)、光照 (4) 和噴灑農藥 (5)。

科學家要選擇可使標準差盡可能小，而使信噪比和斜率盡可能大的因子水準。範例，對於品種，水準 1 的全部實驗的平均標準差為 0.7794，而水準 2 的全部實驗的平均標準差為 0.5042。這表明水準 1 使標準差最小化。下表顯示對每個因子和反應特徵而言最佳的因子水準。可以看到品種和肥料的最佳水準並不合意。要瞭解科學家如何解決此問題，請參見《預測田口結果的 StatGuide》。

分析田口設計 > 圖表 - 主要效應圖  

主要效應圖顯示每個因子如何影響反應特徵。當因子的不同水準對特徵產生不同影響時，即存在主要效應。對於有兩個水準的因子，可能會發現一個水準會提高平均值，而另一個水標準不然。這種差異就是主要效應。

Minitab 透過繪製每個因子水準的特徵平均數來建立主要效應圖。這些平均數與反應表中顯示的那些平均數相同。以線連接每個因子的各個點。檢視此線可以確定對某個因子是否存在主要效應。

·    當線為水準時（與 x 軸平欄），則不存在主要效應。因子的每個水準以相同的方式影響特徵，且全部因子水準中的特徵平均數都相同。

·    當線不水準時（與 x 軸不平欄），則存在主要效應。不同因子水準對特徵的影響不同。描繪點之間垂直位置的差異越大（線與 X 軸不平欄的程度越大），主要效應的量值就越大。

透過比較線的斜率，可以比較因子效應的相對量值。

輸出範例

解釋

對於羅勒資料，顯示了信噪比的主要效應圖。此圖表明下列內容：

·    肥料對信噪比的影響最大。肥料 2 的實驗的信噪比比肥料 1 的實驗高得多。

·    噴灑農藥對信噪比幾乎沒有影響，因為其近似於水準線。

分析田口設計 > 圖表 - 交互作用圖  

田口設計傳統上關心主要效應，但檢定可疑的交互作用也很重要。使用交互作用圖確定某個因子對反應特徵的影響是否依賴於另一個因子的水準。

Minitab 透過為兩個因子繪製每個因子水準組合的特徵平均數來建立交互作用圖。因此，對於各自有兩個水準的兩個因子，將繪製四個點以表示四個可能的組合。某個因子的水準在水準軸上表示，而另一個因子的水標準由不同色彩的線和符號來表示。

·    如果線彼此平欄，則兩個因子之間沒有交互作用。

·    如果線彼此不平欄，則兩個因子之間存在交互作用。

評估變更某個因子如何影響反應時，必須考慮交互作用。

·    不存在交互作用時，比較容易解釋因子效應。然後，主要效應圖和反應表顯示變更某個因子水準的同時使其它因子保持穩定會如何影響反應特徵。

·    如果存在交互作用，則主要效應不再反映因子的實際效應。取決於其它因子的水準，效應可能有各種方向。

輸出範例

解釋

對於羅勒資料，變異數分析表表明品種與肥料之間的交互作用對任何反應特徵都不顯著。檢視交互作用圖時應考慮這一事實。在圖中，實線表示品種 1，虛線表示品種 2。顯示了信噪比的交互作用圖。

對於信噪比，線幾乎是平欄的。品種 2 的信噪比比使用肥料 1 和 2 的品種 1 更高。對於品種 2，肥料 2 產生的信噪比要高於肥料 1 的信噪比。

分析田口設計 > 圖表 - 散佈圖  

動態反應實驗的散佈圖顯示針對信號繪製的反應。每個單元都顯示實驗中因子設定之一的全部資料。單元內容如下所示：

·    繪製了透過參考點的最小平方迴歸線。

·    每個儲存格上方的欄號指的是工作表欄號，即該單元的因子設定所出現的第一欄。

·    實驗的信噪比、斜率和標準差位於單元的下。

圖表按信噪比的降序順序排欄，以便最先繪製「最佳」實驗。如果實驗具有九個實驗以上，則會顯示散佈圖的多個圖表視窗。

檢視散佈圖時需要注意的事項有：

·    配適線是否緊密符合「最佳」實驗的資料模式？觀測的離差是何種類型？

·    資料的模式是直線還是曲線？如果是直線，它服從適配直線還是偏移？

·    是否存在任何異常反應值或異常值？資料在直線附近的散佈在最佳適配與最差適配之間是否存在重大差異？

輸出範例

解釋

對於羅勒資料，資料的散佈在最佳適配和最差適配之間存在重大差異。

·    在第一個單元的圖（對應於欄 21）中，資料非常接近於直線。

·    在左下角的圖（對應於欄 9）中，資料的變化範圍要大得多。

在某些情況下，範例欄 9 的圖，似乎在每個信號水準都有一個點遠遠偏離於其它點之下。確定此偏離是否在全部資料範圍內對相同噪聲條件都出現將很有價值。資料並不曲率。正如可能預期的是，資料的散佈隨信號水準而增加。

分析田口設計 > 圖表 - 殘差的直方圖  

殘差的直方圖顯示全部觀測值的殘差異布。使用直方圖作為研究工具來瞭解資料的下列特徵：

·    典型值、波動或變異以及形狀

·    資料中的異常值

殘差的直方圖應該為鍾形。使用此圖尋找下列資訊：

此圖表趨勢...                         表明...

長尾                                        偏斜度

遠離其他長條的長條            異常值

由於直方圖的外觀會根據用於對資料進行分組的區間數而變更，因此請使用常態機率圖和適合度檢定來評定殘差是否為常態。

輸出範例

解釋

對於羅勒資料，由於觀測值數量太少，因此無法確定是否有證據表明存在偏斜度或異常值。

分析田口設計 > 圖表 - 殘差的常態圖  

此圖表圖示當分布為常態時的殘差及其期望值。根據分析得出的殘差應該是常態分布的。實際上，對於平衡或接近平衡的設計，或者對於具有大量觀測值的資料，略微偏離常態性不會嚴重影響結果。

殘差的常態機率圖應該大致為一條直線。使用此圖尋找下列資訊：

此圖表趨勢...         表明...

非直線                    非常態性

尾部為曲線            偏斜度

遠離直線的點        異常值

斜率不斷變化        未確定的變數

輸出範例

解釋

對於羅勒資料，殘差並不沿直線。由於觀測值數量太少，因此無法確定是否有證據表明存在非常態性、偏斜度、異常值或未確定的變數。

分析田口設計 > 圖表 - 殘差與適配  

此圖表圖示殘差與適配。殘差應該在 0 附近隨機分散。使用此圖尋找下列資訊：

此圖表趨勢...                                                 表明...

殘差相對適配呈扇形或不均勻分散            異變異數

曲線                                                                缺少高次項

遠離 0 的點                                                  異常值

輸出範例

解釋

從這些圖中可以看出，殘差隨機分散在 0 附近。沒有證據表明存在異變異數、缺項或異常值。

分析田口設計 > 圖表 - 殘差與順序  

此圖表以相應觀測值的順序圖示殘差。觀測值的順序可能影響結果時此圖會很有用，以時間順序或以某些其他順序（如地理區域）採集資料時可能影響結果。此圖在試驗未被隨機化的設計實驗中尤其有協助。

圖中的殘差應該在中心線附近隨機波動。檢查此圖以檢視相鄰誤差項之間是否存在任何相關性。殘差之間的相關性可以表示為：

·    殘差中的上升或下降趨勢

·    相鄰殘差的符號快速變化

輸出範例

解釋

對於羅勒資料，殘差可能並不隨機分散在 0 附近。應檢視是否有證據表明誤差項彼此相關。

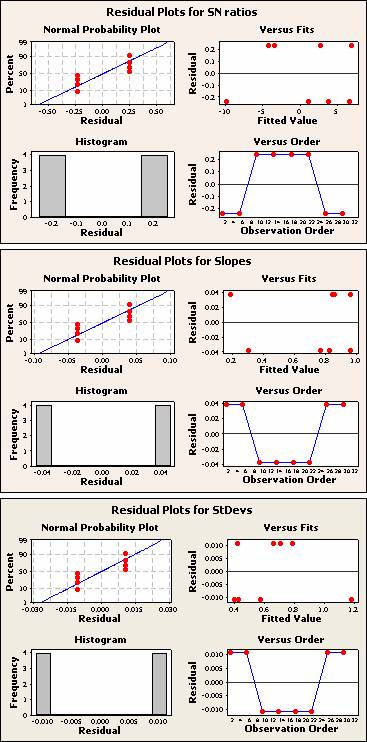
分析田口設計 > 圖表 - 四合一殘差圖  

四合一殘差圖在一個圖表視窗中同時顯示四種不同的殘差圖。此版面有助於比較這些圖以確定模型是否符合分析的假設。此圖表中的殘差圖包含：

·    直方圖 - 表明資料是否偏斜或資料中是否存在異常值

·    常態機率圖 - 表明資料是否為常態分布的、其他變數是否影響反應或資料中是否存在異常值

·    殘差與適配 - 表明變異數是否恆定、是否存在非線性關係或資料中是否存在異常值

·    殘差與資料順序 - 表明資料中是否存在因時間或資料採集順序而產生的系統化影響

輸出範例

解釋

要檢視四合一圖中每個殘差圖的解釋，請參考本主題之前每種殘差圖的個別值主題。

DOE > Taguchi > Analyze Taguchi Design > more

兩步最佳化

典型穩健性參數設計研究的目標是找出可使某些理想目標值（或動態反應實驗情況下的目標函數）的反應變異最小化的因子設定。田口法透過兩步最佳化製程來實現此目的。第一步集中於使變異最小化，第二步集中於實現目標。

·    首先，設定在信噪比最大化的水準對信噪比具有顯著影響的全部因子。

·    然後，調整顯著影響平均值（或斜率）但不影響信噪比的一個或多個因子的水準，以使反應達到目標。

備選方法是以使標準差最小化開始，然後調整影響平均值但不影響標準差的因子。

動態反應實驗與靜態反應實驗

使用 Minitab 可以同時執行動態反應實驗和靜態反應實驗。

·    動態反應實驗：用於最佳化輸入（信號）和輸出（反應）之間的關係。理想關係為線性，且通常反應應該與信號成比例。

一般而言，當品質特徵按照系統輸入作用於一系列值時，使用動態實驗。信號因子的一個熟悉的例子是收音機上的音量旋鈕。反應（即收音機的音量）與音量旋鈕設定的關係應該一致。

對於動態反應實驗，分析以每個因子設定的信號反應資料的最佳配適線為基礎。

·    靜態反應實驗：預期反應只有一個恆定值時使用。在靜態反應實驗中，目標是使有關固定目標的反應的變異性最小化。

對於靜態實驗，分析以每個因子設定的平均反應為基礎。

有關交互作用的更多資訊

在兩個因子中，如果一個因子對反應的作用取決於另一個因子的水準，則這兩個因子存在交互作用。因子 A 和因子 B 之間的交互作用表示為 AB。

範例，假定您可以從兩條路線駕車回家。一條是高速公路，另一條是輔路。兩條路線的距離大致相同，但高速公路的限速要高得多。當交通不擁堵時，高速公路的用時要比輔路少得多。但在交通高峰時，在高速公路上欄駛要緩慢得多，以至於在輔路上欄駛實際上更快一些。

非高峰時段            高峰時段

高速公路                30 分鐘

1 小時

輔路                        45 分鐘

45 分鐘

這是兩個因子（路線和一天中的時段）之間交互作用的一個例子，而反應是回家所需時間。實際上，這是交互作用最極端的形式，其中一個結果的方向會隨另一個因子的水準而變化。如果高速公路始終是最快速的路線，但在高峰時段優勢有所降低，則這種情況仍可以被看作是一個交互作用。

田口正交表設計主要用於研究無交互作用的因子。田口法的提倡者已提供了選擇因子和反應的原則以使交互作用最小化。通常這要求深刻理解實驗系統所涉及的物理製程。

當認為可能存在交互作用或不確定是否存在交互作用時，應選擇可以檢測出交互作用的設計。

什麼是信噪比

信噪比是由田口所設計用於最佳化產品或製程的穩健性的量測。在動態設計中有一個信噪比，而在靜態設計中，取決於根據設計的目標，可以從四個信噪比中進行選擇。應該使用工程知識、對製程的理解以及經驗來選擇合適的信噪比。

靜態設計的信噪比如下所示：

動態設計的信噪比基於標稱最佳信噪比。公式為：

10 log (Slope/MSE)，其中 MSE 是均方誤差，它是量測反應與最佳配適線距離的平方的平均數。

什麼是殘差

Minitab 提供三種類型的殘差：

·    常規殘差：觀測值 - 預測值。

·    標準化殘差：常規殘差 / 常規殘差的標準差。

標準化消除了資料點位置對於預測值或因子的影響。

·    學習化已刪除殘差：對於 ith 資料點，公式遵循與標準化殘差相同的表達方式。但是，計算第i個 學習化已刪除殘差時適配和標準差都是在刪除第i個觀測後得到的。與標準化殘差相比，學習化已刪除殘差在出現異常資料點時會變大。

模型假設

迴歸和變異數分析製程關於誤差做出下列假設：

·    誤差為常態分布，且平均值為 0。

·    誤差變異數不會為不同因子水準或根據預測反應的值而發生變更。

·    每種誤差都獨立於全部其他誤差。在所設計的實驗中，獲得獨立誤差的最好方式是隨機化實驗的實驗順序。

在分析中檢定這些假設的有效性。殘差是誤差的最佳估計值。因此，可以使用殘差圖以圖表方式檢查每個假設。

如果模型違反這些假設，則分析的結果可能有誤導性。範例，如果誤差相互關聯，則可能會錯誤地估計係數的標準誤差，從而導致錯誤的 t 值和 p 值。

直方圖和常態性

下列是從常態分布中抽取的九個資料集樣本。這些樣本沒有問題；但是，這些直方圖中大多數看起來不是鍾形，這描述了為什麼不應該使用直方圖來判斷資料的常態性。判斷資料是否為常態分布需要使用常態機率圖。

隨機產生樣本的直方圖

每個樣本包含常態分布中的 24 個觀測值。

轉換反應變數

殘差表示異變異數或非常態性時，必須進行轉換。

您可能還會發現在模型表現出顯著缺適性時資料轉換非常有用，而且這種轉換在反應曲面實驗的分析中尤為重要。假設在模型中包含全部顯著的交互作用和二次項，但缺適性檢定表明需要高次項。轉換可以消除缺適性。

如果資料轉換修正了此問題，使用迴歸分析比用其他可能更複雜的分析方法要好一些。迴歸分析或實驗設計分析的結果可以指導我們選擇合適的資料轉換方法解決不同的問題。

Box-Cox 轉換是最常用的變異數穩定轉換。在下面第一個圖表中，殘差表示異變異數。第二個圖表顯示變異數穩定轉換之後的殘差。適配的刻度（x 軸）變更，而變異數變為恆定。

常態機率圖中的圖表趨勢

下列圖表趨勢違反了誤差為常態分布這一假設。

非常態性的效應

迴歸和變異數分析的一個假設為殘差來自常態分布。但是，如果設計僅有固定因子，設計為平衡或接近平衡，且具有相當多的觀測值，則略微偏離常態性不會嚴重影響結果。

發現非常態圖表有趨勢時該怎麼做

可能難以正確指出常態機率圖中明顯偏離常態性的原因。可能的原因包含：

·    齊次變異數假設失敗

·    殘差異常大（異常值）

·    模型中缺少重要變數

·    資料來自非常態總體

對於完整分析，請將常態機率圖與其他診斷圖以及適合度統計量結合使用。

如果發現非常態圖表趨勢：

1    使用其他診斷圖檢視非常態性是否由非常態總體中的資料之外的因素所導致。

2    使用統計 > 基本統計 > 常態性檢定來執行常態性檢定。

3    如果確定資料來自非常態總體，則可以在繼續分析之前轉換資料。請參見轉換反應變數。

注意

 修復不等變異數問題的轉換通常也修復常態性問題。

殘差與適配圖中的圖表趨勢

下列圖表趨勢顯示異常值和對誤差為恆定這一假設的衝突。

異常值圖

右上角的殘差比圖中其他全部都大很多，因此為異常值。如果異常值過多，則模型可能不妥當。異常值可能是由於量測錯誤所導致。應該調查異常值以確定其原因。

異變異數圖

殘差的變異數隨適配增加。請注意，隨著適配的增加，殘差在零殘差線周圍分散得更廣，指明不等的（非恆定）變異數。此圖表趨勢表明誤差變異數隨平均值的增加而增加。資料的轉換會有助於穩定這些變異數。

發現圖表有趨勢時該怎麼做

如果圖顯示...                 執行此操作...

異變異數                        1    使用統計 > 變異數分析 > 變異數相等檢定來檢定相等變異數的假設。

2    如果圖或檢定表明變異數不等，則考慮轉換反應變數。

異常值或有影響的點    1    驗證觀測值不是量測或資料錄入錯誤。

2    考慮執行分析時不包含此觀測值來檢視它是否影響結果。

缺少高次項                    增加此項並重新適配模型。

殘差與順序圖中的圖表趨勢

下列圖表趨勢違反了誤差彼此獨立這一假設。

隨著觀測值的順序從左到右提高，殘差系統地降低。

殘差的值從低（左）到高（右）急劇變化。

發現圖表有趨勢時該怎麼做

殘差與資料順序圖中的圖表趨勢表明誤差不是獨立的。此指示可能嚴重影響分析的結論，因此應該至少考慮下列一種補救措施：

·    由於誤差的非獨立性往往難以修正，因此如果要進行設計的實驗，應該盡量透過隨機化試驗以防止出現這種問題。

·    向模型中增加時間效應以消除誤差項的相關。範例，正在檢視幾個月期間的日收入。增加表示一周中某天的因子會消除誤差項中的非獨立性。

·    考慮時間序列製程（如 ARIMA）以解決誤差項中的自相關。

詳細資訊請到官方網站進一步了解: http://www.minitab.com.tw/ 和 http://www.minitab.com/

聲明: 本文純粹學術性研討, 內容所提及任何關於 Minitab 專有創作文字, 圖像與架構…等皆屬Minitab Inc. 版權所有, 嚴禁商業上轉貼使用.