Minitab: 6 sigma 專業軟體 繁體中文討論-83

有學過6 sigma的同學, 一定知道 Minitab這套軟體, 因為它把6 sigma實用化了. 過去 Minitab 並沒有中文版, 但對岸有人將它漢化後, 官方也出簡體中文版, 使用簡體中文版會比英文版更friendly, 但畢竟兩岸語文還是有差異, 尤其專有名詞上的差異更讓人難以適從, 例如常態分配 v.s. 正态分布; 品質 v.s. 质量; 巨集 v.s. 宏; 變異數分析 v.s.方差分析; 進階 v.s. 高级…

官方目前沒有繁體中文版.~可惜! 希望 Minitab TWN公司能早日完成繁體中文版的 Minitab. ~期待!

        先前談到 Tutorials 教學課程, 了解如何使用 Minitab 各項功能。而在Help 協助 > StatGuide 統計指南中, 則對於輸出的結果有詳細的解釋說明:

Regression > Stepwise Regression

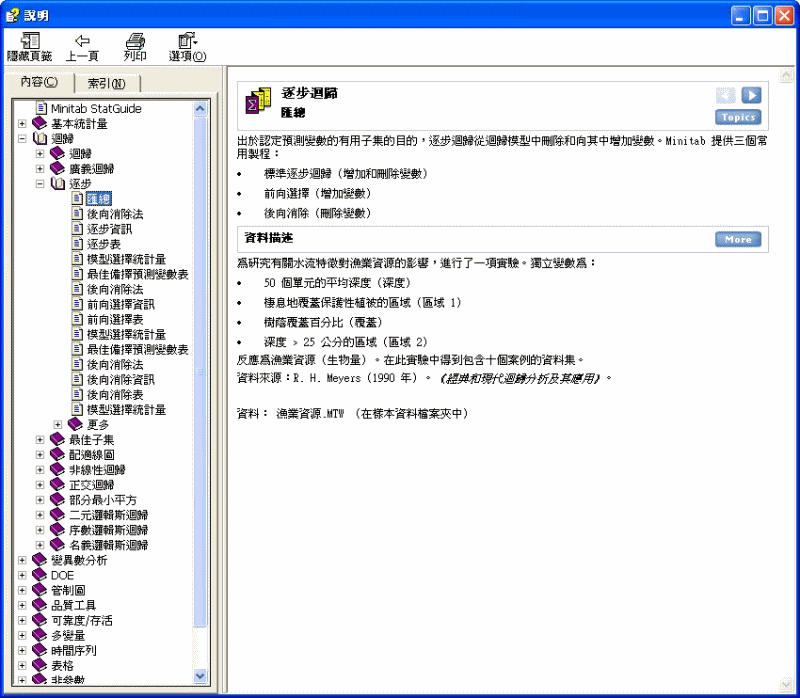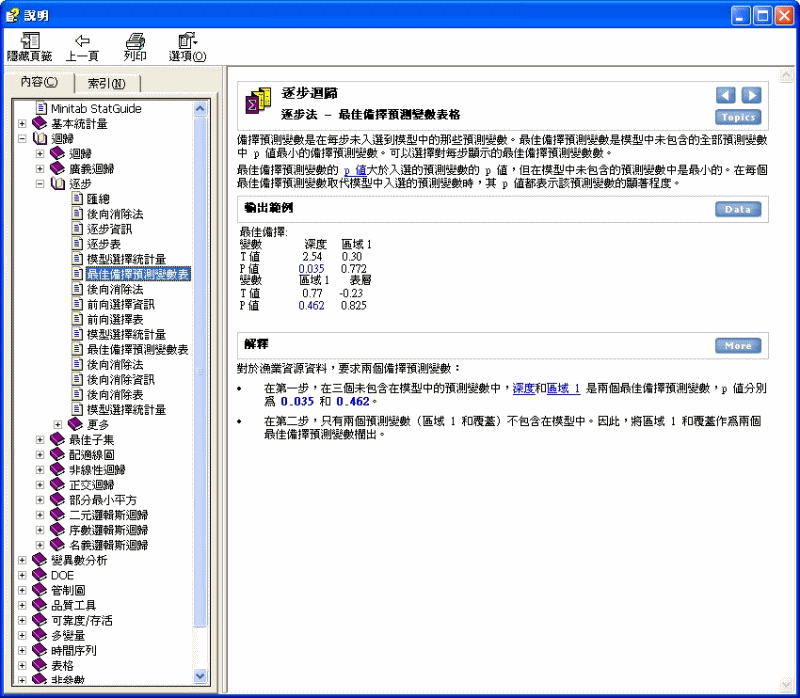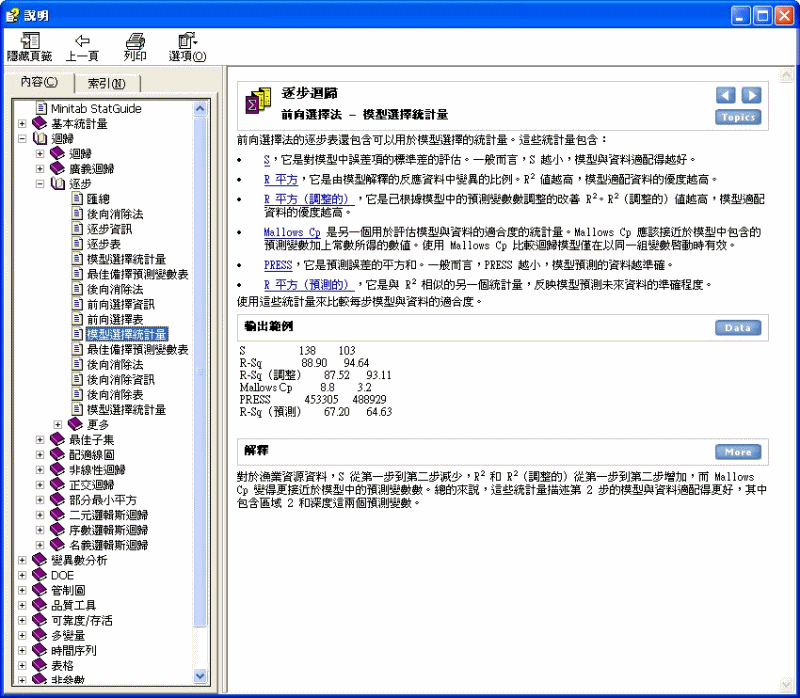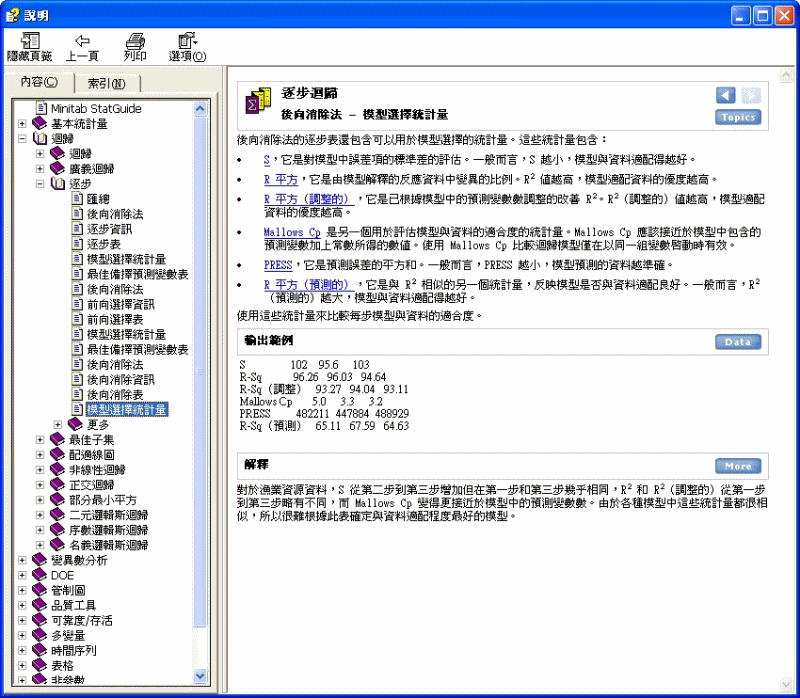
逐步迴歸 > 匯總   

出於認定預測變數的有用子集的目的，逐步迴歸從迴歸模型中刪除和向其中增加變數。Minitab 提供三個常用製程：

·    標準逐步迴歸（增加和刪除變數）

·    前向選擇（增加變數）

·    後向消除（刪除變數）

資料描述

為研究有關水流特徵對漁業資源的影響，進行了一項實驗。獨立變數為：

·    50 個單元的平均深度（深度）

·    棲息地覆蓋保護性植被的區域（區域 1）

·    樹蔭覆蓋百分比（覆蓋）

·    深度 > 25 公分的區域（區域 2）

反應為漁業資源（生物量）。在此實驗中得到包含十個案例的資料集。

資料來源：R. H. Meyers（1990 年）。《經典和現代迴歸分析及其應用》。

資料： 漁業資源.MTW （在樣本資料檔案夾中）

逐步迴歸 > 逐步法 - 逐步資訊  

逐步迴歸是透過根據指定的入選用 Alpha 和刪除用 Alpha 值在模型中包含或排除變數來產生模型的製程。逐步資訊表包含：

·    入選用 Alpha，此值用於確定是否應將模型中當前所沒有的預測變數增加到模型。

·    刪除用 Alpha，此值用於確定是否應將模型中的預測變數從模型中刪除。

·    匯總欄，其中包含分析中的反應名稱、所考慮的獨立變數或預測變數數以及所使用的觀測值數。

輸出範例

  入選用 Alpha: 0.15  刪除用 Alpha: 0.15

反應為 4 個自變數上的 生物量，N = 10

解釋

以漁業資源為例，入選用 Alpha 和刪除用 Alpha 都是 0.15。因此，在製程的每一步，如果在 p 值小於 0.15 的預測變數中，某預測變數的 p 值最小，則將該預測變數增加到模型中。同樣地，在製程接下來的每步，如果預測變數在 p 值大於 0.15 的預測變數中具有最大的 p 值，則只從模型中刪除該預測變數。

對於漁業資源資料，反應是生物量，並且有 4 個預測變數和 10 個案例。

逐步迴歸 > 逐步法 - 逐步表  

此表基於入選用 alpha 值顯示逐步模型選擇在每一步的結果。逐步表還包含所包含的預測變數的係數、t 值和 p 值。p 值用於確定是將預測變數入選到模型中，還是從模型中刪除預測變數。

輸出範例

步驟                  1          2

常數              48.09     197.91

區域 2             2.12       2.96

T 值               8.01       8.08

P 值              0.000      0.000

深度                         -13.1

T 值                         -2.74

P 值                         0.029

解釋

對於漁業資源資料，選擇預測變數只要使用兩步：

·    在第一步，區域 2 擁有小於 0.15（入選用 Alpha 值）的最小 p 值。因此，區域 2 是入選到模型中的第一個預測變數。

·    在第二步，深度具有小於 0.15 的最小 p 值，因此深度是入選到模型中的第二個預測變數。在本模型中，區域 2 的係數是 2.96，t 值是 8.08，p 值是 0.000。

·    第二步之後，模型外就沒有 p 值小於 0.15 的預測變數了，而模型中也沒有 p 值大於 0.15 的預測變數。因此，任何預測變數都不能入選到模型中或從模型中刪除。最終模型包含兩個預測變數：區域 2 和深度。

逐步迴歸 > 逐步法 - 模型選擇統計量  

逐步表包含可以用於模型選擇的統計量。這些統計量包含：

·    S 用於估計模型中誤差項的標準差。一般而言，S 越小，模型與資料適配得越好。

·    R 平方是由模型解釋的反應資料中變異的比例。R 值越高，模型適配資料的優度越高。

·    R 平方（調整的） 表示已根據模型中項數調整的改善 R。

·    Mallows Cp 是另一個用於評估模型與資料的適合度的統計量。Mallows Cp 應該接近於模型中包含的預測變數加上常數所得的數值。使用 Mallows Cp 比較迴歸模型僅在以同一組變數啟動時有效。

·    PRESS 是預測誤差的平方和。一般而言，PRESS 越小，模型預測的資料越準確。

·    R 平方（預測的）是與 R 相似的另一個統計量，反映模型預測未來資料的準確程度。

使用這些統計量來比較每步模型與資料的適合度。

輸出範例

S                   138        103

R-Sq              88.90      94.64

R-Sq（調整）      87.52      93.11

Mallows Cp          8.8        3.2

PRESS            453305     488929

R-Sq（預測）      67.20      64.63

解釋

對於漁業資源資料，S 從第一步到第二步減少，R 和 R（調整的）從第一步到第二步增加，而 Mallows Cp 變得更接近於模型中的預測變數數。總的來說，這些統計量描述第 2 步的模型與資料適配得更好，其中包含區域 2 和深度這兩個預測變數。請注意，PRESS 增加且預測 R 減少，這描述此模型可能無法很好地預測未來資料。如果要對預測使用模型，則有不同預測變數的模型可能更合適。

逐步迴歸 > 逐步法 - 最佳備擇預測變數表格  

備擇預測變數是在每步未入選到模型中的那些預測變數。最佳備擇預測變數是模型中未包含的全部預測變數中 p 值最小的備擇預測變數。可以選擇對每步顯示的最佳備擇預測變數數。

最佳備擇預測變數的 p 值大於入選的預測變數的 p 值，但在模型中未包含的預測變數中是最小的。在每個最佳備擇預測變數取代模型中入選的預測變數時，其 p 值都表示該預測變數的顯著程度。

輸出範例

最佳備擇:

變數               深度     區域 1

T 值               2.54       0.30

P 值              0.035      0.772

變數             區域 1       表層

T 值               0.77      -0.23

P 值              0.462      0.825

解釋

對於漁業資源資料，要求兩個備擇預測變數：

·    在第一步，在三個未包含在模型中的預測變數中，深度和區域 1 是兩個最佳備擇預測變數，p 值分別為 0.035 和 0.462。

·    在第二步，只有兩個預測變數（區域 1 和覆蓋）不包含在模型中。因此，將區域 1 和覆蓋作為兩個最佳備擇預測變數欄出。

逐步迴歸 > 前向選擇法 - 前向選擇資訊  

使用前向選擇法的逐步迴歸透過在模型中包含基於指定的入選用 Alpha 的變數來產生模型。在前向選擇中，預測變數入選到模型中後，將再也不會將其從模型中刪除。逐步資訊表包含：

·    入選用 Alpha，此值用於確定是否應將模型中當前所沒有的預測變數增加到模型。

·    匯總欄，其中包含分析中的反應名稱、所考慮的獨立變數或預測變數數以及所使用的觀測值數。

輸出範例

前進法。  入選用 Alpha: 0.15

反應為 4 個自變數上的 生物量，N = 10

解釋

對於漁業資源資料，入選用 Alpha 為 0.15。因此，在製程的每一步，如果在 p 值小於 0.15 的預測變數中，某預測變數的 p 值最小，則將該預測變數增加到模型中。

對於漁業資源資料，反應是生物量，並且有 4 個預測變數和 10 個案例。

逐步迴歸 > 前向選擇法 - 前向選擇表  

此表基於入選用 alpha 值顯示前向模型選擇在每一步的結果。前向選擇逐步表包含每步所包含的預測變數的係數、t 值和 p 值。p 值用於確定預測變數是否入選到模型中。

輸出範例

步驟                  1          2

常數              48.09     197.91

區域 2             2.12       2.96

T 值               8.01       8.08

P 值              0.000      0.000

深度                         -13.1

T 值                         -2.74

P 值                         0.029

解釋

對於漁業資源資料，選擇預測變數只要使用兩步：

·    在第一步，區域 2 擁有小於 0.15（入選用 Alpha 值）的最小 p 值。因此，區域 2 入選到模型中。

·    在第二步，深度具有小於 0.15 的最小 p 值，因此深度是入選到模型中的第二個預測變數。在本模型中，區域 2 的係數是 2.96，t 值是 8.08，p 值是 0.000。

·    第二步之後，模型外就沒有 p 值小於 0.15 的預測變數了。因此，任何預測變數都不能入選到模型中。最終模型包含兩個預測變數：區域 2 和深度。

逐步迴歸 > 前向選擇法 - 模型選擇統計量  

前向選擇法的逐步表還包含可以用於模型選擇的統計量。這些統計量包含：

·    S，它是對模型中誤差項的標準差的評估。一般而言，S 越小，模型與資料適配得越好。

·    R 平方，它是由模型解釋的反應資料中變異的比例。R 值越高，模型適配資料的優度越高。

·    R 平方（調整的），它是已根據模型中的預測變數數調整的改善 R。R（調整的）值越高，模型適配資料的優度越高。

·    Mallows Cp 是另一個用於評估模型與資料的適合度的統計量。Mallows Cp 應該接近於模型中包含的預測變數加上常數所得的數值。使用 Mallows Cp 比較迴歸模型僅在以同一組變數啟動時有效。

·    PRESS，它是預測誤差的平方和。一般而言，PRESS 越小，模型預測的資料越準確。

·    R 平方（預測的），它是與 R 相似的另一個統計量，反映模型預測未來資料的準確程度。

使用這些統計量來比較每步模型與資料的適合度。

輸出範例

S                   138        103

R-Sq              88.90      94.64

R-Sq（調整）      87.52      93.11

Mallows Cp          8.8        3.2

PRESS            453305     488929

R-Sq（預測）      67.20      64.63

解釋

對於漁業資源資料，S 從第一步到第二步減少，R 和 R（調整的）從第一步到第二步增加，而 Mallows Cp 變得更接近於模型中的預測變數數。總的來說，這些統計量描述第 2 步的模型與資料適配得更好，其中包含區域 2 和深度這兩個預測變數。

逐步迴歸 > 前向選擇法 - 最佳備擇預測變數表  

備擇預測變數是在每步未入選到模型中的那些預測變數。最佳備擇預測變數是模型中未包含的全部預測變數中 p 值最小的備擇預測變數。可以選擇對每步顯示的最佳備擇預測變數數。

最佳備擇預測變數的 p 值大於入選的預測變數的 p 值，但在模型中未包含的預測變數中是最小的。在每個最佳備擇預測變數取代模型中入選的預測變數時，其 p 值都表示該預測變數的顯著程度。

輸出範例

最佳備擇:

變數               深度     區域 1

T 值               2.54       0.30

P 值              0.035      0.772

變數             區域 1       表層

T 值               0.77      -0.23

P 值              0.462      0.825

解釋

對於漁業資源資料，要求兩個最佳備擇預測變數：

·    在第一步，在三個未包含在模型中的預測變數中，深度和區域 1 是兩個最佳備擇預測變數，p 值分別為 0.035 和 0.462。

·    在第二步，只有兩個預測變數（區域 1 和覆蓋）不包含在模型中。因此，將區域 1 和覆蓋作為兩個最佳備擇預測變數欄出。

逐步迴歸 > 後向消除法 - 後向消除資訊  

逐步迴歸的後向消除法以包含全部預測變數的模型開始。根據指定的刪除用 Alpha 一次一個地刪除預測變數。對於後向消除法，將預測變數從模型中刪除後，它就無法再次入選。後向消除表包含：

·    刪除用 Alpha，此值用於確定是否應將模型中的預測變數從模型中刪除。

·    匯總欄，其中包含分析中的反應名稱、所考慮的獨立變數或預測變數數以及所使用的觀測值數。

輸出範例

後退法。  刪除用 Alpha: 0.15

反應為 4 個自變數上的 生物量，N = 10

解釋

對於漁業資源資料，刪除用 Alpha 為 0.15。因此，在製程的每一步，如果在 p 值大於 0.15 的預測變數中，某預測變數的 p 值最大，則將該預測變數從模型中刪除。

對於漁業資源資料，反應是生物量，並且有 4 個預測變數和 10 個案例。

逐步迴歸 > 後向消除法 - 後向消除表  

此表基於刪除用 alpha 值顯示後向模型消除在每一步的結果。後向消除表還包含每步模型中所包含的預測變數的係數、t 值和 p 值。p 值用於確定是否從模型中刪除預測變數。

輸出範例

步驟               1       2       3

常數           85.75  137.53  197.91

深度           -15.9   -15.2   -13.1

T 值           -3.10   -3.25   -2.74

P 值           0.027   0.018   0.029

區域 1           2.4     2.1

T 值            1.47    1.45

P 值           0.202   0.198

表層             1.8

T 值            0.56

P 值           0.603

區域 2          3.07    3.03    2.96

T 值            8.22    8.80    8.08

P 值           0.000   0.000   0.000

解釋

對於漁業資源資料，選擇預測變數要使用三步：

·    在第一步，適配包含全部預測變數的模型。

·    在第二步，覆蓋擁有大於 0.15（刪除用 Alpha 值）的最大 p 值(0.603)。因此，將覆蓋從模型中刪除，並且按反應迴歸其餘的預測變數。在本模型中，區域 2 的係數是 3.03，t 值是 8.80，p 值是 0.000。

·    在第三步，區域 1 擁有大於 0.15 的最大 p 值 (0.198)。因此，將區域 1 從模型中刪除，並且按反應迴歸其餘的預測變數。

·    第三步之後，模型中剩餘的全部預測變數的 p 值就都小於 0.15 了。最終模型包含兩個預測變數：區域 2 和深度。

逐步迴歸 > 後向消除法 - 模型選擇統計量  

後向消除法的逐步表還包含可以用於模型選擇的統計量。這些統計量包含：

·    S，它是對模型中誤差項的標準差的評估。一般而言，S 越小，模型與資料適配得越好。

·    R 平方，它是由模型解釋的反應資料中變異的比例。R 值越高，模型適配資料的優度越高。

·    R 平方（調整的），它是已根據模型中的預測變數數調整的改善 R。R（調整的）值越高，模型適配資料的優度越高。

·    Mallows Cp 是另一個用於評估模型與資料的適合度的統計量。Mallows Cp 應該接近於模型中包含的預測變數加上常數所得的數值。使用 Mallows Cp 比較迴歸模型僅在以同一組變數啟動時有效。

·    PRESS，它是預測誤差的平方和。一般而言，PRESS 越小，模型預測的資料越準確。

·    R 平方（預測的），它是與 R 相似的另一個統計量，反映模型是否與資料適配良好。一般而言，R（預測的）越大，模型與資料適配得越好。

使用這些統計量來比較每步模型與資料的適合度。

輸出範例

S                102    95.6     103

R-Sq           96.26   96.03   94.64

R-Sq（調整）   93.27   94.04   93.11

Mallows Cp       5.0     3.3     3.2

PRESS         482211  447884  488929

R-Sq（預測）   65.11   67.59   64.63

解釋

對於漁業資源資料，S 從第二步到第三步增加但在第一步和第三步幾乎相同，R 和 R（調整的）從第一步到第三步略有不同，而 Mallows Cp 變得更接近於模型中的預測變數數。由於各種模型中這些統計量都很相似，所以很難根據此表確定與資料適配程度最好的模型。

Regression > Stepwise Regression > more

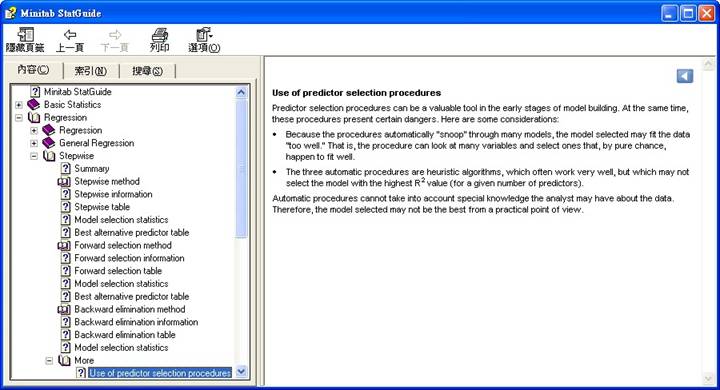
預測變數選擇製程的使用

在模型構建的早期階段，預測變數選擇製程可以作為一種很有價值的工具。但同時，這些製程也表現出一定的危險。下列是一些注意事項：

·    由於這些製程自動「監聽」多種模型，因此所選的模型可能會與資料「過度」適配。也就是說，製程可以檢視許多變量，並完全出於偶然地選擇了恰好適配良好的變數。

·    三個自動製程都是啟髮式算法，通常試驗很好，但可能所選模型的 R 值（對於給定的預測變數數）並非最高。

自動製程無法考慮到分析人員可能具有的有關資料的特殊知識。因此，從實際觀點來看，所選模型可能不是最佳模型。

詳細資訊請到官方網站進一步了解: http://www.minitab.com.tw/ 和 http://www.minitab.com/

聲明: 本文純粹學術性研討, 內容所提及任何關於 Minitab 專有創作文字, 圖像與架構…等皆屬Minitab Inc. 版權所有, 嚴禁商業上轉貼使用.